در حوزه یادگیری ماشین و یادگیری عمیق، الگوریتمهای هوش مصنوعی مختلفی وجود دارند که از هر کدام میتوان در حل مسائلی خاص استفاده کرد. شبکه عصبی «پرسپترون چند لایه» (Multi Layer Perceptron | MLP) به عنوان یکی از انواع شبکههای عصبی مصنوعی پرکاربرد محسوب میشود و از آن میتوان در حل مسائل پیچیدهای استفاده کرد که در آنها شبکه عصبی پرسپترون تک لایه کاربرد ندارد.
در این مطلب از مجله فرادرس قصد داریم در ابتدا به توضیح مختصری از شبکه پرسپترون تک لایه بپردازیم تا خواننده با ساختار کلی پرسپترون آشنا شود. سپس، اجزای درونی مدل پرسپترون چند لایه را شرح میدهیم و به ویژگیها و کاربردهای آن اشاره خواهیم کرد. در پایان مطلب نیز مثالی از زبان برنامه نویسی پایتون ارائه خواهیم داد تا مخاطب این مطلب با نحوه پیادهسازی این مدل در پایتون آشنا شود.
شبکه عصبی تک لایه پرسپترون چیست؟
مدل تک لایه پرسپترون یک شبکه عصبی ساده است که توسط «فرانک رزنبلات» (Frank Rosenblatt) در دهه ۱۹۵۰ ارائه شد. این مدل لایه پنهان ندارد و از آن به منظور دستهبندی داده ورودی در دو کلاس استفاده میشود. میتوان مدل تک لایه پرسپترون را جزء الگوریتمهای «یادگیری نظارت شده» (Supervised Learning) تلقی کرد که آن را برای دستهبندی خطی دادهها به کار میبرند.
شبکه عصبی پرسپترون تک لایه محاسباتی را بر روی ورودی خود انجام میدهد تا دادهها را بر اساس شناسایی ویژگیهایشان، در دو کلاس جای دهد. به همین خاطر، به این مدل، دستهبند دودویی خطی نیز گفته میشود.
مدل پرسپترون تک لایه از ۴ بخش تشکیل شده است:
- مقادیر ورودی یا لایه ورودی: لایه ورودی پرسپترون تک لایه از نورونهایی ساخته شده است که دادهها را دریافت میکنند و این مقادیر را برای پردازش به لایه بعد میفرستند.
- وزنها و بایاس: پارامترهای شبکه عصبی، وزنها و مقدار بایاس هستند و هدف آموزش شبکههای عصبی، پیدا کردن این مقادیر است. وزنهای شبکه، مقدار اهمیت ورودی متناظر را مشخص میکند.
- جمع مقادیر وزندار ورودی: مقدار دادههای ورودی در وزنهای شبکه ضرب و در نهایت با مقدار بایاس با یکدیگر جمع میشوند تا مقدار نهایی، به تابع فعالسازی ارسال شود.
- «تابع فعالسازی» (Activation Function): مقدار خروجی مرحله قبل از یک تابع خطی عبور میدهد تا مقدار خروجی شبکه مشخص شود. این تابع خطی، تابع فعالسازی نام دارد. در مدل پرسپترون تک لایه، از توابع فعالسازی نظیر Heaviside استفاده میشود. این تابع، به ازای مقادیر بزرگتر مساوی ۰، مقدار ۱ و به ازای مقادیر کوچکتر از ۰ مقدار ۰ را در خروجی برمیگرداند.
در تصویر زیر، نمونهای از شبکه عصبی پرسپترون تک لایه را به همراه محاسبات درون آن ملاحظه میکنید.
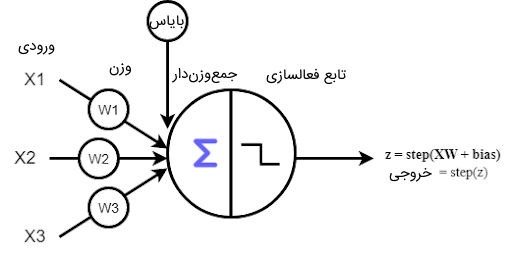
مشکل پرسپترون تک لایه چیست؟
مدل پرسپترون تک لایه، مدل سادهای است که صرفاً میتواند دادهها را در دو کلاس قرار دهد و دستهبندی دادهها را بهصورت خطی انجام دهد. به دلیل چنین محدودیتی، نمیتوان از این مدل در مسائل پیچیدهتر استفاده کرد. به همین خاطر، در دهه ۱۹۸۰ «جفری هینتون» (Geoffrey Hinton) با بررسی مغز انسان دریافت که مغز از یک مجموعه پیچیدهای از نورونهای متصل به هم ساخته شده است که میتواند محاسبات پیچیدهای بر روی دادهها انجام دهد. وی از مشاهدات خود به این نتیجه رسید که مدل پرسپترون تک لایه را میتواند همانند مغز انسان به مدل چند لایه تبدیل کند تا از آن بتوان در حل مسائل پیچیدهتر و غیرخطی نیز استفاده کرد. بدین ترتیب، شبکه عصبی پرسپترون چند لایه ظهور پیدا کرد.
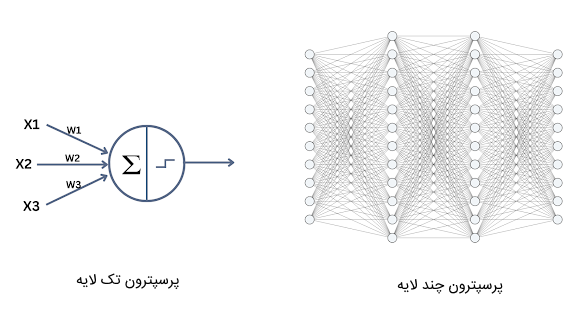
در ادامه، به توضیح شبکه عصبی چند لایه پرسپترون و ویژگیهای آن میپردازیم.
شبکه عصبی پرسپترون چند لایه
مدل پرسپترون چند لایه به عنوان یکی از انواع شبکههای عصبی تلقی میشود که از چندین لایه نورون متصل به هم تشکیل شده است. در این نوع شبکه عصبی، بر خلاف سایر الگوریتم های یادگیری عمیق نظیر «شبکه عصبی بازگشتی» (Recurrent Neural Network | RNN)، دادهها صرفاً به یک جهت (به سمت جلو) در شبکه منتقل میشوند. از مدل پرسپترون چند لایه در طراحی سایر الگوریتمهای هوش مصنوعی مانند «شبکه عصبی پیچشی» (Convolutional Neural Network | CNN) استفاده میشود.
به منظور درک عملکرد شبکه پرسپترون چند لایه میتوان از یک مثال ساده کمک گرفت. فرض کنید ۵ دانشآموز ۷ ساله داریم که میخواهند یک مسئله ریاضی را حل کنند. این دانشآموزان فقط میتوانند محاسبات ساده دو رقمی را انجام دهند. اما مسئله ریاضی مطرح شده به این صورت است:
? = ۵ * ۳ + ۲ * ۴ + ۸ * ۲
از آنجایی که دانشآموزان نمیتوانند این مسئله ریاضی را حل کنند، باید آن را به بخشهای کوچکتری تقسیم کرد و هر بخش را به یک دانشآموز داد تا در نهایت پاسخ مسئله مشخص شود. به عنوان مثال، میتوان از دانشآموز اول درخواست کرد که محاسبه ۲ * ۸ را انجام دهد. دانش آموز دوم و سوم نیز بهترتیب میتوانند حاصل ۲ * ۴ و ۳ * ۵ را به دست آورند. از دانشآموز بعدی میتوانیم درخواست کنیم پاسخ دانشآموز اول و پاسخ دانشآموز دوم را با یکدیگر جمع کند. سپس، دانشآموز آخر نیز میتواند پاسخ دانشآموز سوم و چهارم را با هم جمع کند تا مقدار نهایی مسئله به دست آید.
بدینترتیب، با شکستن صورت مسئله ریاضی به بخشهای کوچکتر و حل هر یک از آنها میتوان به پاسخ نهایی مسئله رسید. این دقیقاً همان ایدهای است که شبکه عصبی پرسپترون چند لایه برای حل مسائل پیش میگیرد. هر نورون مدل، به عنوان یک دانشآموز عمل میکند و محاسبات ساده ریاضی را انجام میدهد. پاسخ نهایی هر نورون به نورونهای بعدی منتقل میشود تا در نهایت، پاسخ مسئله حاصل شود.
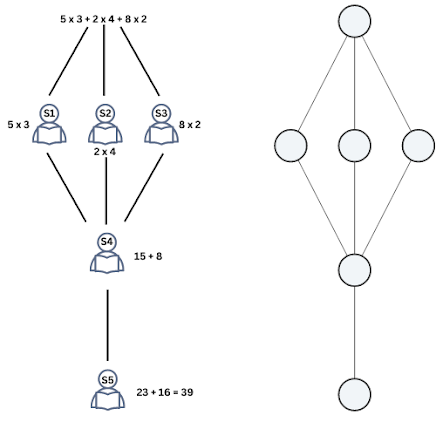
ساختار شبکه عصبی چند لایه پرسپرتون
شبکه عصبی پرسپترون چند لایه از چندین لایه متصل به هم تشکیل شده است. در ادامه، به لایههای این مدل اشاره میکنیم:
- لایه ورودی: این لایه، اولین لایه شبکه عصبی است که دادههای ورودی را دریافت میکند و وظیفه آن، ارسال دادهها به لایه بعدی است.
- لایه پنهان: لایههای پنهان میتوانند بیش از یک لایه باشند. این لایهها از نورونهایی تشکیل شدهاند که وظیفه انجام محاسباتی را بر روی ورودیهای خود بر عهده دارند و خروجی حاصل شده از محاسبات را به لایه بعد خود منتقل میکنند.
- لایه خروجی: این لایه، مقدار خروجی نهایی شبکه را مشخص میکند. ورودی این لایه، خروجیهای لایه پنهان است.
تعداد نورونهای لایه ورودی شبکه پرسپترون چند لایه برابر با اندازه دادههای ورودی است و تعداد نورونهای لایه خروجی، برابر با تعداد دستههای تعریف شده برای مسئله است. هر چقدر تعداد لایههای میانی (لایه پنهان) بیشتر باشد، شبکه نهایی میتواند از پس مسائل پیچیدهتری برآید.
پردازش داده ها در شبکه عصبی پرسپترون چند لایه
همانطور که در بخش پیشین مطلب حاضر از مجله فرادرس گفته شد، مدل پرسپترون چند لایه از سه لایه اصلی ورودی، لایه پنهان و لایه خروجی تشکیل شده است. زمانی که دادهها را به ورودی این شبکه ارسال میکنیم، دادهها از لایه ورودی عبور میکنند. در این لایه، هیچگونه محاسباتی بر روی دادهها انجام نمیشود و لایه ورودی صرفاً مسئولیت انتقال دادهها را به لایه بعدی بر عهده دارد.
نورونهای لایه پنهان، بر روی دادههای دریافتی محاسباتی را انجام میدهند و سپس مقادیر حاصل شده را به لایه بعدی خود منتقل میکنند. این روند انتقال دادهها تا زمانی پیش میرود که دادهها به لایه آخر منتقل شوند.
نورونهای لایههای پنهان با یک سری مقادیر (وزنهای شبکه) به یکدیگر متصل هستند که میزان اهمیت نورون را برای پردازش دادهها مشخص میکند. هر چقدر وزنها بیشتر باشند، تاثیر نورون متصل به آن وزن در محاسبه بیشتر است و در پی این اتفاق، آن نورون بر روی محاسبه خروجی مسئله تاثیر بیشتری خواهد گذاشت. از طرف دیگر، اگر وزن یک نورون خیلی کوچک باشد، تاثیر داده آن نورون در محاسبات بعدی شبکه کمتر خواهد بود و در نتیجه تغییرات چندانی در خروجی نهایی شبکه ایجاد نخواهد کرد.
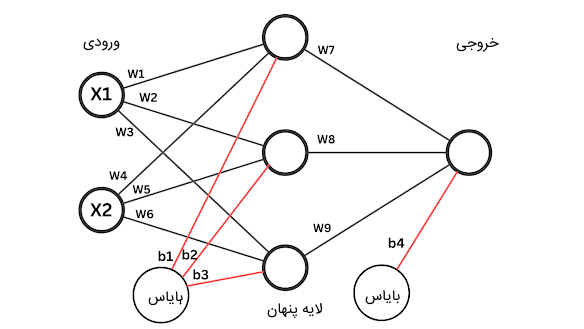
مقدار بایاس هر لایه نیز به نوعی مقدار حد آستانه خروجی یک نورون را مشخص میکند. چنانچه حاصل جمع ورودی یک نورون با بایاس از یک مقدار مشخص بیشتر شود، آن نورون یک مقدار خروجی تولید میکند در غیر این صورت مقدار نهایی حاصل شده آن نورورن برابر با عدد ۰ است. در فرمول زیر، پردازش محاسباتی درون هر نورون را ملاحظه میکنید:
$$ z = WX + bias $$
در این فرمول، W وزنهای شبکه و X ورودیهای شبکه هستند. هر نورون این فرمول را برای خود محاسبه میکند. محاسبات تا به اینجا، مشابه با محاسبات شبکه عصبی پرسپترون تک لایه است. این فرمول برای مدلهای خطی به کار میرود. اما هدف از طراحی مدل پرسپترون چند لایه این بود که مسائل غیر خطی را حل کند. بدین ترتیب، در اینجا نیاز داریم از یک سری توابع غیر خطی به نام توابع فعالسازی استفاده کنیم.
اگر بخواهیم عملکرد توابع فعالسازی را برای شما بهسادگی شرح دهیم، میتوانیم بگوییم این توابع تصمیم میگیرند چه نورونهایی در شبکه فعال باشند و خروجی کدام نورونها نادیده گرفته شوند. توابع فعالسازی نحوه پردازش نورونهای مغز را شبیهسازی میکنند و به شبکه این امکان را میدهند تا روابط پیچیده و غیرخطی بین دادههای ورودی و مقدار خروجی شبکه را یاد بگیرند.
بدینترتیب، مقدار z فرمول ذکر شده در بالا به یک تابع فعالسازی در نورون ارسال میشود و خروجی تابع، به عنوان خروجی نورون محسوب میگردد. مقدار خروجی نورون برای انجام محاسبات به لایه بعدی منتقل میشود.
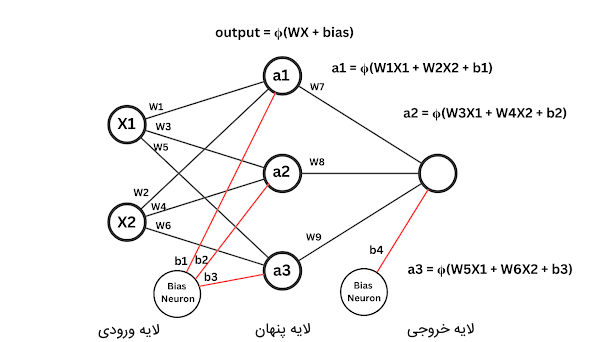
بنابراین، محاسبات هر نورون را با در نظر تابع فعالسازی میتوان بهصورت زیر نوشت:
$$ output = Φ (WX + bias) $$
یا
$$ z = WX + bias $$
$$ output = Φ (z) $$
در فرمول بالا Φ تابع فعالسازی است.
یکی از توابع فعالسازی رایجی که در شبکههای عصبی مورد استفاده قرار میگیرد، تابع «یکسوساز» (Rectified Linear Unit | ReLU) است. این تابع با دریافت مقدار ورودی، بررسی میکند آیا از عدد ۰ بزرگتر هست؟ اگر مقدار ورودی این تابع از عدد ۰ کوچکتر بود، تابع مقدار ۰ را در خروجی باز میگرداند. چنانچه ورودی تابع ReLU از مقدار ۰ بزرگتر بود، تابع مقدار ورودی را به عنوان خروجی برمیگرداند. بازنمایی ریاضی تابع ReLU را در ادامه ملاحظه میکنید:
ReLU = max (0, z)
از توابع فعالسازی دیگری نیز میتوان برای نورونهای شبکه استفاده کرد که در ادامه به برخی از پرکاربردترین آنها اشاره میکنیم:
- تابع فعالسازی «سیگموئید» (Sigmoid): این تابع فعالسازی، مقادیر ورودی خود را به اعدادی بین بازه ۰ تا ۱ نگاشت میکند. از این تابع برای مدلسازی مسائل احتمالاتی استفاده میشود و معمولاً به عنوان تابع فعالسازی لایه آخر شبکه به کار میرود.
- تابع فعالسازی «تانژانت هذلولوی» (Tangent Hyperbolic | Tanh): این تابع فعالسازی، مقادیر ورودی خود را در بازهای بین ۱- و ۱ نگاشت میکند. معمولاً از این تابع در لایههای پنهان استفاده میشود.
- تابع فعالسازی «سافتمکس» (Softmax): این تابع فعالسازی یکی از توابع پرکاربرد برای لایه آخر شبکه عصبی است و از آن برای دستهبندی دادههای چندکلاسه استفاده میشود.
پس از این که تمام محاسبات لایه میانی و لایه آخر شبکه MLP انجام شد، بر اساس مقدار خروجی شبکه، میزان خطای مدل محاسبه میشود که در طی یادگیری شبکه، باید این میزان خطا به حداقل مقدار برسد. به منظور بهروزرسانی وزنهای شبکه، با استفاده از «روش پس انتشار» (Backpropagation) از «تابع زیان» (Loss Function | Cost Function) نسبت به وزنهای شبکه مشتق جزئی گرفته میشود و مقادیر وزنها تغییر میکنند.
کاربردهای مدل پرسپترون چند لایه
از مدل عمیق چند لایه پرسپترون در حل مسائل مختلفی استفاده میشود که در این بخش به رایجترین کاربردهای آن اشاره میکنیم:
- تشخیص تصویر: یکی از کاربردهای رایج مدل MLP استفاده از آن در تشخیص الگوهای موجود در تصاویر است تا با کمک این اطلاعات، تصاویر را در دستههای مختلف قرار دهد. این امر در مسائلی نظیر تشخیص چهره، تشخیص اشیا، قطعهبندی تصاویر و سایر مسائل پردازش تصویر کاربرد دارد.
- «پردازش زبان طبیعی» (Natural Language Processing | NLP): از شبکه عصبی چند لایه پرسپترون برای درک و تولید زبان انسان استفاده میشود. کاربرد این مدل عمیق را میتوان در مسائلی نظیر تبدیل متن به گفتار، ترجمه ماشینی و تحلیل احساسات ملاحظه کرد.
- مدلسازی پیشبینی: از شبکه MLP میتوان برای پیشبینی مسائل بر پایه دادههای موجود استفاده کرد. کاربرد مدلسازی پیشبینی را میتوانیم در مسائلی نظیر پیشبینی بورس، پیشبینی وضعیت آب و هوا و تشخیص کلاهبرداری ببینیم.
- تشخیصهای پزشکی: از مدل MLP میتوان در حوزه پزشکی به منظور تشخیص بیماریهای مختلف استفاده کرد. تفسیر تصاویر پزشکی یکی از کارهایی است که بهراحتی با استفاده از مدل پرسپترون چند لایه با دقت بالا انجام میشود.
- سیستمهای پیشنهاد دهنده: از شبکه عصبی MLP میتوان در طراحی سیستمهای پیشنهاد دهنده استفاده کرد تا بر اساس یک سری ویژگیها نظیر سلایق مشتری، خریدهای قبلی مشتری، جستجوهای مشتری و مواردی از این قبیل، پیشنهادات خرید مرتبطی را به مشتری نشان دهد.

مزایای مدل عمیق MLP
مدل هوش مصنوعی پرسپترون چند لایه دارای ویژگیهای مثبتی است که در ادامه به برخی از مهمترین آنها اشاره میکنیم:
- از مدل MLP میتوان برای پیادهسازی مسائل غیرخطی پیچیده استفاده کرد.
- مدل چند لایه پرسپترون میتواند برای مسائلی با حجم داده زیاد نتایج خوبی را ارائه دهد.
- پس از مرحله آموزش، مدل MLP برای پیشبینی درباره دادههای تست به زمان زیادی نیاز ندارد.
- اگر دادههای آموزشی کمی را برای مسئله تهیه کرده باشیم، مدل MLP تقریباً همان نتایجی را ارائه میدهد که با داده زیاد آن را آموزش داده باشیم.
معایب شبکه عصبی MLP
شبکه عصبی MLP علاوهبر مزایا، دارای معایبی نیز هست که در ادامه به آنها میپردازیم:
- این مدل برای رسیدن به همگرایی، به داده، زمان و پارامترهای زیادی احتیاج دارد.
- احتمال رخداد «بیش برازش» (Overfitting) و «کم برازش» (Underfitting) برای این مدل عمیق وجود دارد.
- «محو شدگی گرادیان» (Vanishing Gradients) از دیگر مسائلی است که به عنوان معایب شبکه MLP در نظر گرفته میشود.
- مدل MLP در حین آموزش ممکن است در نقطه مینیم محلی گیر کند. بدینترتیب، این احتمال وجود دارد بهینهترین پاسخ برای مسئله پیدا نشود.
پیاده سازی رگرسیون با استفاده از شبکه MLP در پایتون
در این بخش مطلب از مجله فرادرس، قصد داریم یک مسئله رگرسیون را با مدل پرسپترون چند لایه پیادهسازی کنیم. در این مسئله با استفاده از کتابخانه Numpy زبان برنامه نویسی پایتون، دادههایی را بهشکل تصادفی تولید میکنیم و با استفاده از مدل MLP قصد داریم الگوهای این دادهها را تشخیص دهیم.
در ابتدا، با استفاده از قطعه کد زیر، دادههای آموزشی را ایجاد میکنیم:
from sklearn.datasets import make_regression
import numpy as np
import matplotlib.pyplot as plt
X_train = np.linspace(-10, 10, 1000)
y_train = np.sin(X_train) + np.random.normal(0, 0.2, size=X_train.shape)
X_test = np.linspace(-10, 10, 500)
y_test = np.sin(X_test) + np.random.normal(0, 0.2, size=X_test.shape)با کمک قطعه کد زیر، دادههای تولید شده را در قالب نمودار ملاحظه میکنیم:
plt.scatter(X_train, y_train)
plt.show()خروجی قطعه کد بالا در تصویر زیر قابل ملاحظه است:
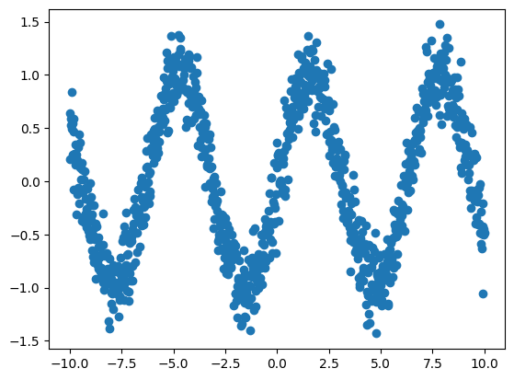
با استفاده از «تنسورفلو» (Tensorflow) و «کراس» (Keras)، مدل پرسپترون چند لایه را به صورت زیر تعریف میکنیم:
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Dense(62, activation='relu', input_dim=1))
model.add(tf.keras.layers.Dense(62, activation='relu'))
model.add(tf.keras.layers.Dense(1, activation='linear'))در قطعه کد بالا ملاحظه میکنید که شبکه عصبی MLP دارای دو لایه پنهان است که هر کدام از لایهها، ۶۴ نورون با تابع فعالسازی ReLU دارند. ابعاد داده ورودی برابر با ۱ است زیرا دادههای آموزشی تنها دارای یک ویژگی هستند و لایه آخر این شبکه نیز دارای یک نورون است.
model.compile(loss='mse', optimizer='adam', metrics=['mae'])
history = model.fit(X_train, y_train, epochs=500)تابع هزینه مسئله رگرسیون را از نوع Mean Square Error یا همان MSE در نظر گرفتیم و برای بهینهسازی مدل نیز از الگوریتم بهینه سازی آدام Adam استفاده کردیم. قطعه کد زیر نیز نحوه عملکرد مدل را بر روی دادههای آموزشی نشان میدهد:
plt.scatter(X_train, y_train)
plt.plot(X_train, model.predict(X_train), color='red')
plt.show()خروجی قطعه کد بالا به صورت زیر است. منحنی قرمز رنگ به عنوان منحنی رگرسیون با استفاده از مدل MLP شکل گرفته است.
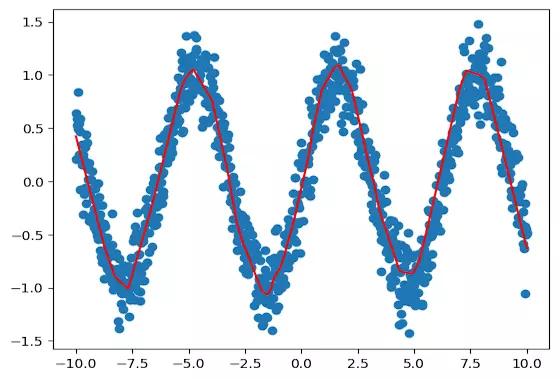
با استفاده از قطعه کد زیر نیز از مدل برای پیشبینی مقادیر دادههای تست استفاده میکنیم:
pred = model.predict(X_test)
plt.scatter(X_test, y_test)
plt.plot(X_test, pred, color='red')
plt.show()خروجی قطعه کد بالا را در تصویر زیر ملاحظه میکنید:
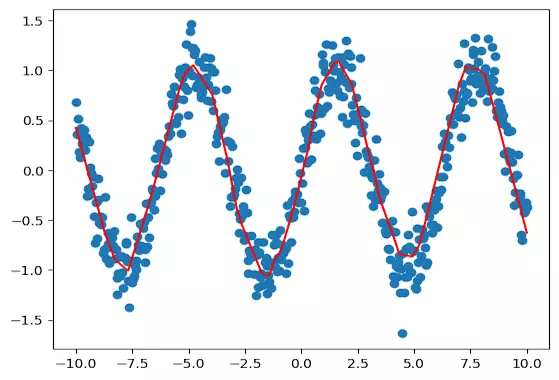
جمعبندی
الگوریتمهای مختلفی در حوزه ماشین لرنینگ و یادگیری عمیق وجود دارند که با توجه به ویژگیهای منحصربهفردی که دارند، در مسائل خاصی استفاده میشوند. در مطلب حاضر از مجله فرادرس، به توضیح شبکه عصبی پرکاربرد پرسپترون چند لایه پرداختیم که این مدل در ساختار سایر مدلهای عمیق نیز کاربرد دارد. این مطلب شامل توضیح کاملی از ساختار درونی شبکه عصبی MLP بود و به ویژگیها و مزایا و معایب آن نیز اشاره شد. در نهایت، یک مثال از مسئله رگرسیون ارائه گردید و نحوه استفاده از مدل پرسپترون چند لایه را برای پیادهسازی این مسئله شرح دادیم.
source